L1 正则为何导致稀疏性

L1 正则与 L2 正则的区别是一个老生长谈的问题。我记得自己刚读研究生时就对这个问题感兴趣，实验室也常有同学讨论。

那时的理解比较浅显，主要从梯度的角度来看这个问题的。L1 正则项和 L2 正则项都在原点取得极值，但各自对输入的导数却不同。 L1 正则项的梯度恒为 1 ，在优化过程中，所有变量会同时以 1 的速率趋于极值点； L2 正则项梯度的大小与自身成比例，值越大，趋近零的速率就越快，结果就是最后所有变量都很接近且在零附近。

上面的解释也只是说明了一些 L2 正则化的特性，但不能对 L1 正则化为何导致稀疏性这个问题作答。后面我查阅资料，在《统计学习基础》这本书中找到了答案。

要说的直观点，我们回到简单的 Lasso 回归问题上：

$$\begin{array}{}\text{(1)}& {\hat{\beta }}^{\mathrm{lasso}}=& \underset{\beta }{\mathrm{argmin}}\sum _{i=1}^N{(y_i-{\beta }_0-\sum _{j=1}^p{x}_{ij}{\beta }_j)}^2\text{(2)}& & \mathrm{subject}\mathrm{to}\sum _{j=1}^p|{\beta }_j|\le t.\end{array}$$

它是一个带约束条件的凸优化问题，可以用拉格朗日算子法求解。在二维情形，其优化可用下图的左子图示意。

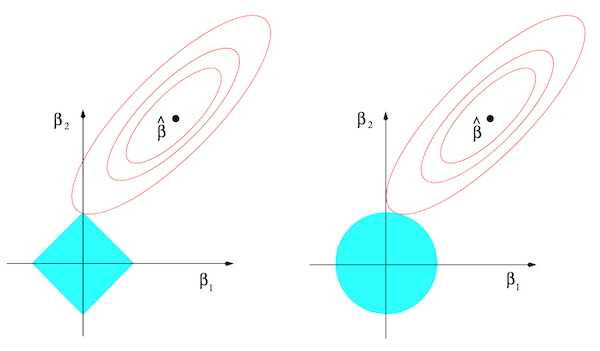
方形表示约束区域，红线是优化函数性能曲面的等高线，两者边界接触那点就是该优化问题的解。我们可以看到，L1 正则的约束区域是方形，其角所对应的解就是某种程度的稀疏解（解的某些维度为 0）。对比 L2 正则的右子图，由于左子图的约束区域是方形（有角），其角处的区域更容易（概率更大）与优化函数性能曲面的等高线优先接触。因此最后也就更容易得到稀疏解。在高维情况下，这种概率会更大，因为高维的超方体很像一个浑身长满尖刺的海胆。

如果对最后一点有疑问，推荐看下这篇文章： Why does L1 regularization encourage coefficients to shrink to zero?。文章里有很多直观的动画帮助理解，自己也是看了其生动直观的动画才有感而发。