R3GAN: A Modern Baseline GAN

对抗式生成网络 (GAN) 可以在一次前向传递中生成高质量的图像，但也存在训练不稳定和模型坍塌等问题。目前 GAN 在与 Diffusion model 的竞争中已落入下风。 这篇 NIPS 2024 上的论文 (1) 从 GAN 的目标损失函数和网络结构两个方面进行改进，提出了一个网络结构简单且训练稳定的 GAN 基线。

首先回顾 GAN 最初的损失函数：

\[\mathcal{L}(\theta,\psi)=\mathbb{E}_{z\thicksim p_z}\left[f\left(D_\psi(G_\theta(z))\right)\right]+\mathbb{E}_{x\thicksim p_\mathcal{D}}\left[f\left(-D_\psi(x)\right)\right].\]

该损失函数通常会将假样本移出 \(\mathcal{D}\) 设定的决策边界，而不是直接更新密度函数 \(p_{\theta}\)。这种退化情况就对应着模型坍塌，并且这种退化的局部最优解在上述损失函数的性能曲面中广泛存在。

作者接着考察了 RpGAN (2)，其损失函数如下：

\[\mathcal{L}(\theta,\psi)=\mathbb{E}_{z\thicksim p_{z},x\thicksim p_{\mathcal{D}}}\left[f\left(D_\psi(G_\theta(z))-D_\psi(x)\right)\right].\]

RpGAN 通过耦合真实和虚假数据使假样本的真实性根据其耦合的真实样本进行评估，从而有效地在每个真实样本的邻域中保持决策边界，防止模式丢弃。不过实践中发现非正则化 RpGAN 并不总是收敛。文中证明在 RpGAN 的损失函数中引入梯度惩罚 (0-GP) 正则项就能保证收敛。这就得到 R3GAN 的最终损失函数：RpGAN + R1 + R2。

在网络结构这部分，作者用 StyleGAN2 (3) 为基准，裁剪出了一个十分简单的网络结构:

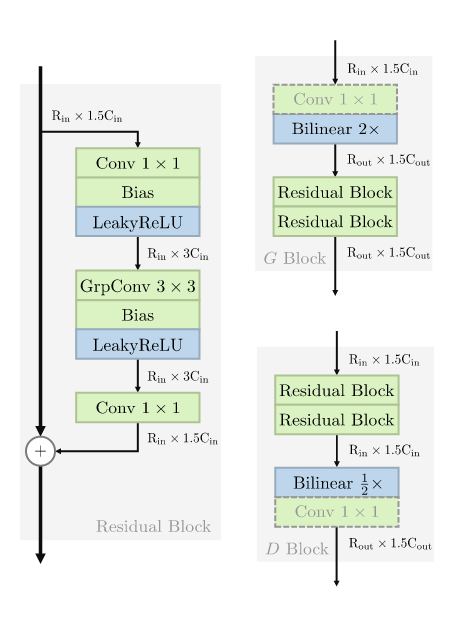
具体的裁剪细节比较繁琐，不再多说。在最后的实验部分中，该基线 GAN 模型在同等参数的情况下取得了与当前 SOTA 模型相当的性能。R3GAN 没有多余的 Tricks 和复杂的网络结构就能取得不错的效果，值得继续研究。